Considere que φ(x) indica a solução para o problema de valor inicial
,
(a) Mostre que φ′′(x) = 1 − φ′(x) = 1 − x + φ(x).
(b) Demonstre que o gráfico de φ está diminuindo para x próximo de zero e que quando x aumenta a partir de zero, φ(x) diminui até cruzar a linha y = x, onde sua derivada é zero.
(c) Considere que x* seja a abscissa do ponto onde a curva solução y = φ(x) cruza a linha y = x. Considere o sinal de φ′′(x*) e demonstre que φ tem um mínimo relativo em x*.
(d) O que você pode dizer sobre o gráfico de y = φ(x) para x > x*?
(e) Verifique se y = x − 1 é uma solução para dy/dx = x − y e explique por que o gráfico de φ(x) sempre permanece acima da linha y = x − 1.
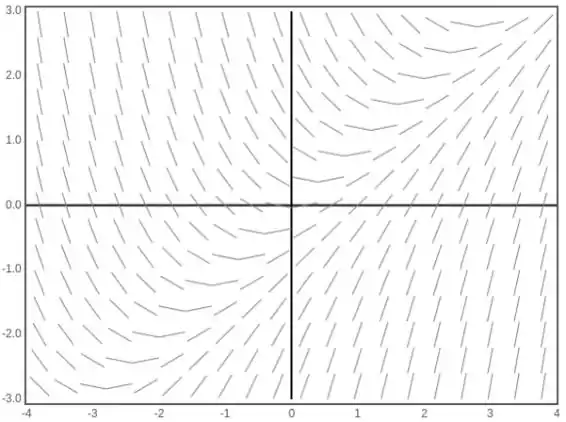
(f) Esboce o campo de direção para dy/dx = x − y usando o método das isóclinas ou um software de computador.
(g) Esboce a solução y = φ(x) usando o campo de direção no item (f).
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- desde é a solução do problema de valor inicial que ela satisfaz:
- Como x é quase zero, (1) se torna:
- Como y=ϕ(x) cruza a linha y=x em x=x*, pode-se ver que em x*:
- Como ϕ tem um mínimo relativo em x*, segue-se que ϕ(x) aumenta para x>x*
- Para y=x−1, segue, . Substituindo isso na equação diferencial inicial:
- Basta digitar "plotadora de campo de direção/inclinação" na barra de pesquisa para encontrar a plotadora desejada.
- Esboce a solução y=x−1, que é uma linha que passa pelos pontos (−1,0) e (0,1), no mesmo campo de direção. Observe que a solução segue as setas.
Além disso, a segunda derivada de ϕ(x) em relação a x usando (1) é:
Substituindo (1) na equação superior, obtemos:
Passo 2
mas sabemos que y(0) = 1, já que ϕ(x) é uma solução de (1), isso significa que ϕ(0) =1, portanto, a primeira derivada é negativa, significando que ϕ(x) é decrescente. Observe também que se xϕ(x), ϕ′(x)>0, significando que ϕ(x) está aumentando.
de (1) nós temos:
Além disso, de (a), temos:
Como ϕ′(x∗)=0 e ϕ′′(x∗)>0, ϕ tem um mínimo relativo em x*.
Passo 3
Finalmente, verifique se y=1−x satisfaz y(0)=1:
Portanto, y=x−1 é uma solução para o problema de valor inicial. Observe que y=x y=x−1 são linhas paralelas, portanto, y=x−1 sempre fica abaixo de x=y. Isso pode ser visto no esboço abaixo.
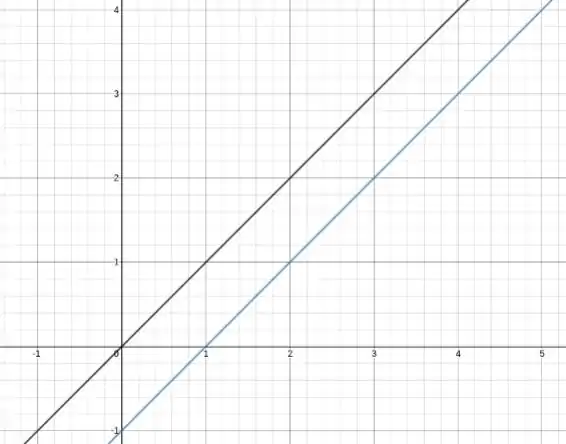
Passo 4
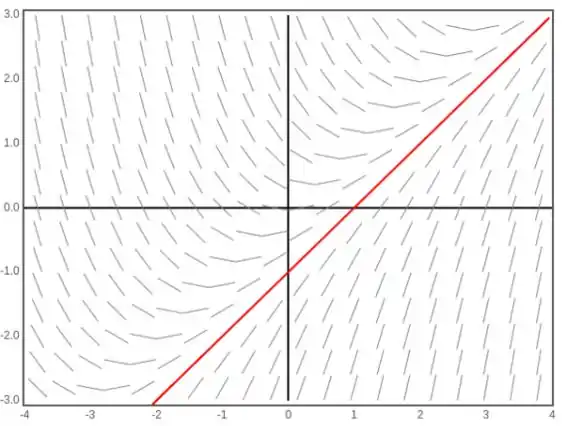
Resposta
- Encontre a segunda derivada para encontrar ϕ′′(x)=1−ϕ′(x)=1−x+ϕ(x).
- Observe que ϕ′(x)0 para x>ϕ(x).
- Mostre que ϕ′(x∗)=0 e ϕ′(′x∗)>0.
- Como ϕ tem um mínimo relativo em x*, segue que ϕ(x) aumenta para x>x*.
- Mostre que satisfaz o problema de valor inicial. Observe que y=x y=x−1 são linhas paralelas.