Considere novamente o problema de valor inicial () do Exemplo . Investigue o quão pequeno tem que ser o tamanho do passo para garantir que o erro em e em seja menor do que .
a) Use o método de Euler.
c Use o método de Runge-Kutta.
c) Use o método de Euler inverso.
Passo 1
Saudações galerinha! Tudo bem?
Vamos juntos resolver mais um exercício?
Bora lá começar então!
Primeiramente vamos relembrar a formula de Euler:
Comparando essas matrizes podemos extrair nossas equações:
Com h=0.1 podemos encontrar os valores das variáveis e organizar em uma tabela:

Até aí tranquilo?

Bora continuar então!
Passo 2
O método Runge-Kutta usa os seguintes cálculos intermediários:
Com h=0.1 podemos encontrar os valores das variáveis e organizar em uma tabela:
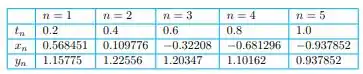
Passo 3
Com o método de Euler invertido devemos tirar a matriz inversa advindas do método de Euler.
Com h=0.1 podemos encontrar os valores das variáveis e organizar em uma tabela:

Te vejo na próxima questão!
Resposta
a)

b)
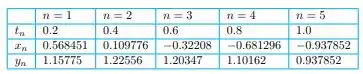
c)
