Considere um peso de w N suspenso por dois fios, conforme mostra a figura a seguir. Se a magnitude do vetor F2 é 100 N, encontre o ângulo w e a magnitude do vetor F1.
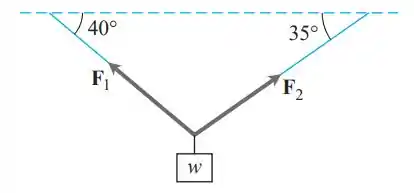
Obs.: Há um erro no enunciado, pois o que é pedido não é o ângulo w, e sim a intensidade da força peso. O ângulo pode ser calculado lembrando que a soma dos ângulos internos de um triângulo é igual a 180⁰.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de vetores e a geometria do espaço.
Vamos agora resolver os exercícios da seção 2 sobre teoria e aplicações de vetores e geometria espacial.
Analisando o enunciado, temos que:
Realizando a soma dos vetores, temos que:
Para o eixo x:
Para o eixo y:
Passo 2
Resolvendo para o eixo x:
Que nos permite reescrever a equação do eixo y:
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.