Considere no plano um campo de forças conservativo , com energia potencial
Uma partícula de massa é abandonada na posição , com velocidade nula.
Olhando apenas para , tente descrever a trajetória descrita pela partícula.
Passo 1
Essa é uma questão que vamos ter que lembrar um pouquinho de física:
O enunciado não disse isso, mas vamos supor que a massa da partícula é . Essa é a única forma de chegarmos no resultado pedido! Portanto,
O primeiro passo é calcular o campo de forças :
Portanto,
Passo 2
Note que a componente da força é e a componente é . Inicialmente, a partícula está em repouso na posição . Assim,
Com isso, a partícula vai se mover aceleradamente ao longo da reta como indicado na figura:
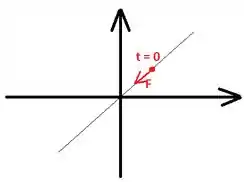
Conforme ela se aproxima da origem, a força diminui de intensidade, se anula em e ao passar para o terceiro quadrante ela muda de sinal:
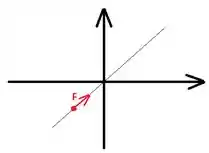
Assim, a partícula vai diminuindo sua velocidade até atingir o repouso no ponto . Daí, ela volta a sem mover se forma acelerada até atingir a origem e retornar ao primeiro quadrante. Essa oscilação vai durar eternamente!
Resposta
Movimento oscilatória ao longa da reta com .