Considere o problema de valor inicial
a) Desenhe urn campo de direções para essa equação. b) Estime ate onde a solução pode ser estendida para a direita. Seja a extremidade direita do intervalo de existencia dessa solução. 0 que acontece em que impede a solução de continuar?. c) Use o método de Runge-Kutta corn diversos tamanhos de passos para encontrar um valor aproximado de . d) Se você continuar os calculos além de você pode continuar a gerar valores de y. Qual o significado (se há algum) desses valores?. e) Suponha que a condição inicial é modificada para y(0) = 1. Repita os itens (b) e (c) para este problema.
Passo 1
Para o item a), vamos fazer o plot via métodos numéricos do campo de direções. O resultado é
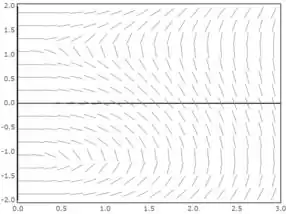
Quanto ao item b), com condição inicial (0,0), plotando o gráfico da solução
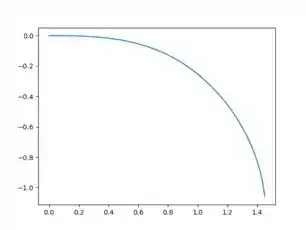
e podemos ver que o limite para temos uma assíntota vertical, ou seja, um limite à direita.
Passo 2
A partir de agora, precisamos utilizar o método de Runge-Kutta. Para diferentes valores de , obtemos os seguintes valores de
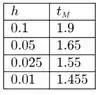
Passo 3
Para o item d), os para valores além de , os valores numéricos continuarão a ser gerados, mas eles não são associados com as curvas integrais em questão. Esses valores são aproximações de curvas integrais próximas. Por fim, no item e), precisamos repetir os itens b) e c), mas mudando a condição inicial para (0,1). O gráfico da solução é dado por
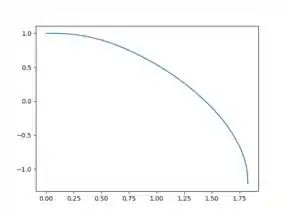
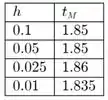
e vemos que agora . Utilizando o método de Runge-Kutta
Resposta
Ei, a resposta está no passo a passo :)