Considere o problema do valor inicial:
a) Encontre a solução ) e desenhe seu gráfico para
b) A análise de estabilidade no texto sugere que para este problema o método de Euler só é estável para . Confirme que isso é verdade aplicando o método de Euler a esse problema para com tamanhos de passos próximos de .
c) Aplique o método de Runge-Kutta a este problema para com diversos tamanhos de passos. 0 que você pode concluir sobre a estabilidade desse método?
d) Aplique o método de Euler inverso a este problema para com diversos tamanhos de passos. Qual o tamanho de passo necessário para que o erro em 5 seja menor do que ?
Passo 1
Saudações galerinha! Tudo bem?
Vamos juntos resolver mais um exercício?
Bora lá começar então!
Primeiramente temos uma EDO com uma solução homogênea dada por:
Podemos determinar a solução particular a partir dos coeficientes da equação:
Substituindo por:
. O valor de C que satisfaz a equação será .
Logo:
Podemos representa essa solução através do gráfico.
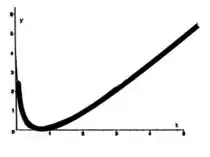
Passo 2
Para esse item devemos levar em consideração a equação 15 apresentada nesta seção. Tranquilo!
Atraves desta equação observamos que deve ser menor que , Para que o método de Euler seja estável devemos ter que
Com h=0.2 podemos encontrar os valores das variáveis e organizar em uma tabela:

Com h=0.18podemos encontrar os valores das variáveis e organizar em uma tabela:

Claramente, o segundo conjunto de valores é estável, embora longe de ser preciso.
Até aí tranquilo?

Bora continuar então!
Passo 3
Aplicando o método Runge-Kutta vamos obter as seguintes valores intermediários
Com h=0.25 podemos encontrar os valores das variáveis e organizar em uma tabela:

Com h=0.28 podemos encontrar os valores das variáveis e organizar em uma tabela:

Com h=0.3 podemos encontrar os valores das variáveis e organizar em uma tabela:

Assim, a instabilidade parece ocorrer em torno de e certamente por . Observe que a solução exata para, então para obtemos um boa aproximação.
Passo 4
Para o erro em , enquanto para , o erro em é .
Te vejo na próxima questão!
Resposta
a)
b)

c)
A instabilidade parece ocorrer em torno de
d) Para o erro em , enquanto para , o erro em é .