Considere o problema de valor inicial
Usando o metodo de Runge-Kutta corn tamanho de passo h, obtemos os resultados na Tabela
8.5.5. Esses resultados sugerem que a solucao tern uma assintota vertical entre t = 0,9 e t = 1,0.

(a) Seja a solucäo do problema (i). Além disso, seja a solucäo do problema
e seja a solução de
Mostre que
em algum intervalo contido em onde existem todas as três soluções. b) Determine e . Depois motre que para algum t entre t = ln 2 0,69315 e t = 1. c) Resolva as equações diferenciais e respectivamente, com a condição inicial . Use os resultados para mostrar que quando t 0,932.
Passo 1
Para o item a) vamos usar o método de Runge-Kutta, vamos utilizá-lo para cálcular o valor das soluções em 5 pontos, no intervalo Para
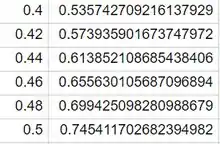
no mesmo intervalo, para
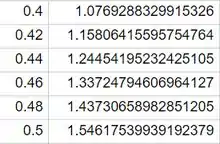
por fim, para
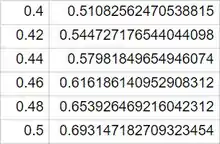
é possível ver que nesse intervalo, temos que .
Passo 2
Para o item b), vamos resolver as equações diferenciais. Começando com :
no lado direito, vamos fazer a substituição , disso tiramos que e que :
resolvendo as integrais:
isso nos fornece
e dessa equação já conseguimos encontrar a nossa constante de integração C. Utilizando da condição inicial , obtemos que C = ln 2. Segue que
colocando exponencial de ambos os lados e usando que
manipulando um pouco
Encontramos então
e podemos reparar que quando y diverge. Para a segunda equação diferencial:
isso nos leva à , colocando nossa condição inicial, obtemos . Daí, isolando y
e a função diverge quando x tende à 1.
Passo 3
O fato de já termos mostrado que as três funções envolvidas no exercício obedecem a uma desigualdade serve de suporte para falarmos que como tende diverge quando x tende a 1 e diverge quando x tende a ln 2, temos que a função deve divergir em algum x no intervalo entre ln 2 e 1.
Para o último item, vamos resolver as equações para a condição inicial indicada. Para
utilizando de , chegamos à C = 2,5392 e portanto
procurando o ponto onde essa função diverge, basta procurarmos por pontos em que o argumento do logaritmo tende a zero. Isso quer dizer que = 0, ou melhor
para o segundo caso, temos
onde, impondo a condição inicial: C = -0,9239 e portanto
e encontramos . Como já argumentamos, o ponto onde a função de interesse diverge, deve estar entre os dois pontos, segue que
Resposta
Ei, a resposta está no passo a passo :)