Construir os gráficos das funções dadas implicitamente:
Passo 1
Espiral logarítmica.
Fazendo:
Então:
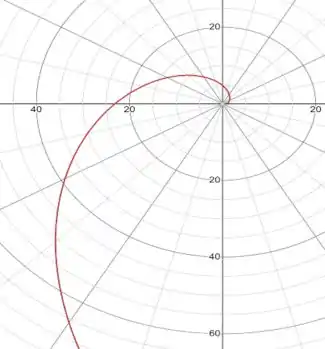
Assim a espiral cresce de forma exponencial.
Resposta
Conseguiu entender a função implícita dada? Achou a mesma curva aí?
Qualquer dúvida manda pra gente!