Construir os gráficos de funções racionais de valor inteiro de grau superior ao segundo:
Passo 1
Vamos conhecer mais um gráfico!
Atribuindo valores para , encontraremos a imagem em , chegando ao seguinte gráfico:
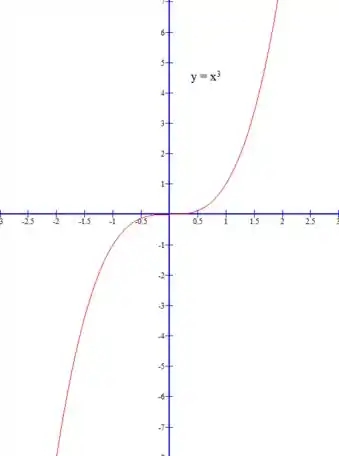
Se reparar bem, a diferença dessa curva para a de uma função do segundo grau se dá para os valores negativos de . Onde, diferente da função de segundo grau, o expoente ímpar não torna os valores positivos, fazendo assim a função decrescer em para .
Resposta
Essa curva também é chamada de parábola cúbica.
Lembra a parábola do segundo grau?