Para a curva logística (15), considere que sejam dados com . Mostre que
[Dica: iguale as expressões (21) para p0 nos instantes ta e tb.
Defina χ = exp (–Ap1ta) e χ2 = exp (–Ap1tb) e resolva para χ.
Insira em uma das expressões anteriores e resolva para p1 .]
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Igualando as expressões (21)) para às vezes e temos
![]()
Configurando χ= e χ²= e resolvendo para χ obtemos
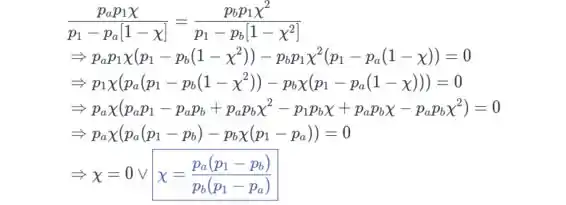
Passo 2
Colocando χ e na equação (21) temos:
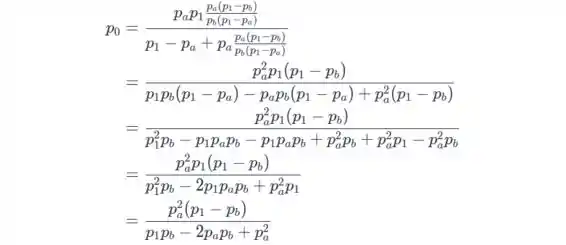
e resolvendo isso para obtemos
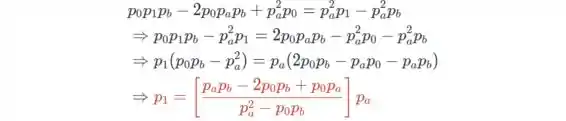
Encontraremos a fórmula para resolver A
![]()
Passo 3
então temos
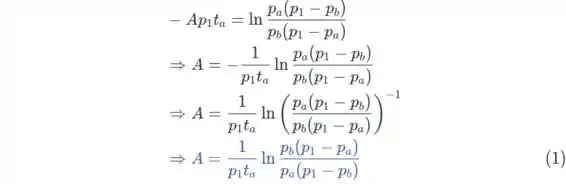
Usando a fórmula para temos

e

Passo 4
Usando as conclusões anteriores obtemos
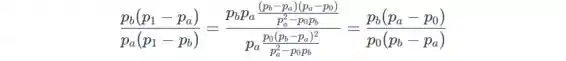
então substituindo isso em (1) nós finalmente temos
![]()
Resposta
Resposta nos passos.