Dada uma esfera de raio R, determinar o raio r e a altura h do cilindro circular reto de maior superfície lateral que pode ser inscrito na esfera.
Passo 1
Desenhando a vista lateral do cilindro inscrito na esfera, temos:
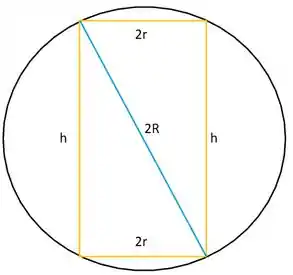
Assim, podemos escrever o seguinte vínculo geométrico:
Além disso, temos que a superfície lateral do cilindro é dada por:
Passo 2
Como queremos maximizar a superfície lateral, podemos derivar SL em função de h e igualar a zero para acharmos os pontos críticos dessa função. O problema é análogo para h ou para r.
Derivando,
Igualando a zero,
Como R e h são positivos,
Passo 3
Utilizando a relação do vínculo geométrico novamente, agora para obter r em função de R, temos:
Resposta
e