Dado um cone circular reto de raio R e altura h, determinar o raio e altura do cilindro circular reto de maior área lateral que pode inscrever-se no cone.
Passo 1
Fala pessoal, blz? O primeiro passo para questões envolvendo maximizar ou minimizar áreas e volumes de duas figuras relacionadas sempre é achar o vínculo geométrico entre as duas figuras.
Nessa questão nós temos um cilindro circular reto dentro de um cone circular reto. Difícil de imaginar? Com certeza, mas o bizu nessas questões não é ficar desenhando o problema em 3D ou perdendo muito tempo imaginando como fica as relações em 3D. A forma mais rápida e fácil de enxergar os vínculos geométricos em questões assim é fazendo a vista lateral.
Como é a vista lateral de um cilindro circular reto? É um retângulo. Com a altura sendo o comprimento desse retângulo e a largura do retângulo sendo 2 vezes o raio da base.
Como é a vista lateral de um cone circular reto? É um triângulo isósceles. Como as geratrizes (parte inclinada) são iguais nos dois lados, o triângulo da vista lateral será isósceles. Além disso, a base do triângulo valerá 2 vezes o raio da base do cone.
Pronto, agora que já sabemos a vista lateral dos dois, como o cilindro está inscrito no cone (cilindro dentro do cone), é só imaginar o retângulo (vista lateral do cilindro) dentro do triângulo (vista lateral do cone).
Assim, podemos desenhar a vista lateral do problema, chamando a altura e o raio do cone de H e R, e a altura e o raio do cilindro de h e r, temos:
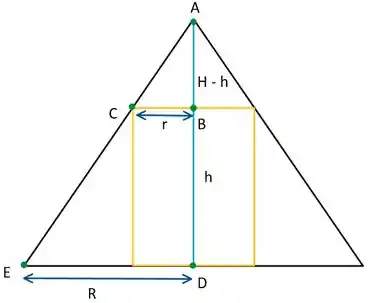
A partir disso, podemos achar o vínculo geométrico da questão enxergando que os triângulos ABC e ADE são triângulos semelhantes, assim:
Passo 2
Agora que já temos o vínculo geométrico entre as figuras, temos que pensar em maximizar a área lateral do cilindro. Para isso, basta derivarmos a expressão da área lateral e igualar ela a zero para achar os pontos críticos da equação. Por fim, vamos testar pra ver se os pontos críticos são máximos ou mínimos.
Área lateral de um cilindro:
Deixando em função de apenas uma variável (utilizando o vínculo geométrico):
Derivando em função de h:
Igualando a zero para acharmos o ponto máximo:
Passo 3
Tendo o h para que a área seja máxima, basta jogarmos no vínculo geométrico para obtermos o r.
Passo 4
Além disso, para a resposta ficar mais completa, precisamos garantir que o ponto crítico achado é um ponto de máximo. Para isso usaremos o conceito da segunda derivada.
Relembrando,
Primeira derivada = 0 🡪 Pontos críticos candidatos a serem pontos de máximo ou de mínimo.
Segunda derivada > 0 🡪 Função convexa (concavidade pra cima) 🡪 Ponto de mínimo.
Segunda derivada
Segunda derivada = 0 🡪 Ponto de inflexão 🡪 Mudança de concavidade, não é nem máximo, nem mínimo.
Assim, fazendo a segunda derivada da função,
Sendo assim, provamos que o ponto encontrado realmente é o ponto onde a função Área lateral é máxima.