Definida a função do modo seguinte:
Passo 1
Vamos traçar o gráfico de para
Basicamente iremos unir o gráfico de com
Para construir o gráfico de basta pegar o gráfico da parábola e “achatar verticalmente”, pois, agora a imagem da função será a metade da imagem de
Gráfico de
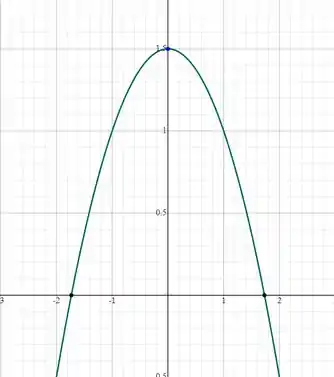
Gráfico de focado no intervalo que queremos: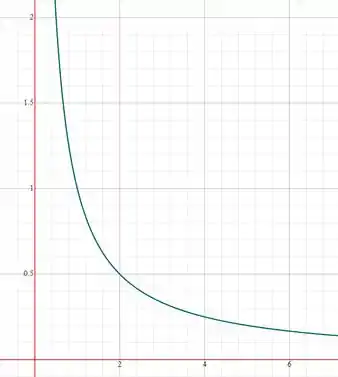
Agora vamos unir os gráficos tirando a parte que não nos interessa:
Resposta Final:
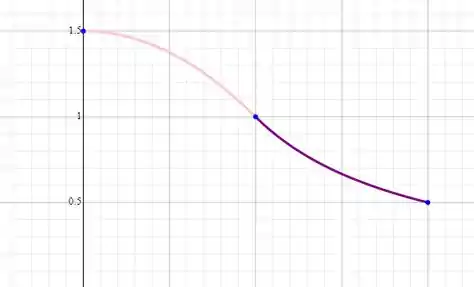
Passo 2
O teorema de Lagrange nos afirma que:
Dada uma função , contínua em e diferenciável em existe um ponto c em tal que:
Pelo gráfico fica claro que é contínua em [0,2] e diferenciável em
Basta acharmos os valores em que vale o teorema, agora:
Passo 3
Agora iremos checar se de fato existe c em
Vamos ver a primeira equação acima
Como c = está no intervalo é válido.
Vamos agora ver a outra equação (
Como não está no intervalo ( não é um valor válido.
Porém c =
Resposta
-
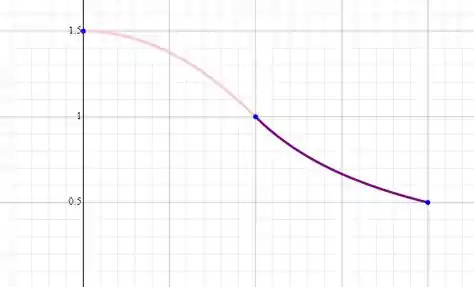
- Pontos x = e x =