Demonstrar que entre todos os retângulos que podem inscrever-se numa circunferência dada, o quadrado é o que tem área máxima.
Passo 1
Primeiramente, vamos desenhar a situação apresentada:
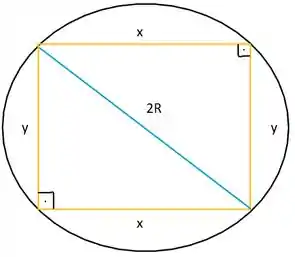
Dessa forma, a área do retângulo será:
Além disso, pelo triângulo retângulo, podemos escrever uma relação entre x e y:
Passo 2
Feito isso, podemos escrever a área em função de apenas uma das variáveis (tanto faz fazer para x ou para y, é análogo).
Passo 3
Para maximizar a área do retângulo, podemos derivar a função área em relação a x e depois igualar a zero para obter o ponto crítico.
Derivando,
Igualando a zero,
Passo 4
Utilizando a relação obtida no passo 1 e a obtida no passo 3, utilizando o teorema de Pitágoras, temos:
Como x e y são positivos,
Logo, provamos que o retângulo inscrito numa circunferência que possui a maior área é um quadrado.
Resposta
Ei, a resposta está no passo a passo :)