Desenhe um campo de direções para a equação diferencial . Baseado no campo de direções , determine o comportamento de quando . Se esse comportamento depender do valor inicial de em . Descreva essa dependência.
Passo 1
Saudações galera! Tudo bem?
Antes de resolver essa questão vamos só lembrar de um detalhe. Beleza!
O campo de direções é o gráfico resultante quando traçamos a inclinação dos valores correspondendo com nossa equação diferencial. Em nosso caso a equação:
Então vamos traçar o gráfico para variando de e variando de
(Esses valores são suficiente para formar nosso campo de direção)
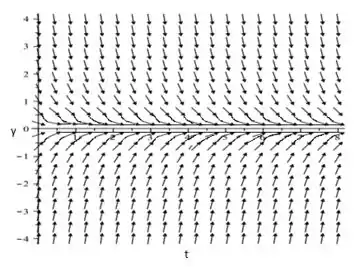
Quando traçarmos o gráfico resultante será:
Passo 2
Para analisar o comportamento da equação diferencial dada no exercício basta apenas observar o campo de direção já traçado anteriormente.
Ao observar seu comportamento analisamos que todos os valores de y estão a assíntota ( se aproximando) do zero. Ou seja
Independente do valor de
Acabamos por aqui!
Te vejo na próxima questão.