Desenhe as superfícies nos Exercícios 13-44.
27.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Fazendo a equação hiperboloide em uma forma padrão para desenhá-la
Passando para a forma canônica
Notando que no plano , nós temos que a hipérbole . No plano nós temos a seguinte hipérbole . Já no plano , nós temos o círculo . Em qualquer plano perpendicular ao eixo ( na equação), temos o círculo .
Passo 2
A partir da discussão acima, a equação dada representa um hiperboloide circular reto de uma folha, ao longo do eixo z e interceptando com o plano e em duas hiperboloides e respectivamente. Portanto, temos o seguinte gráfico
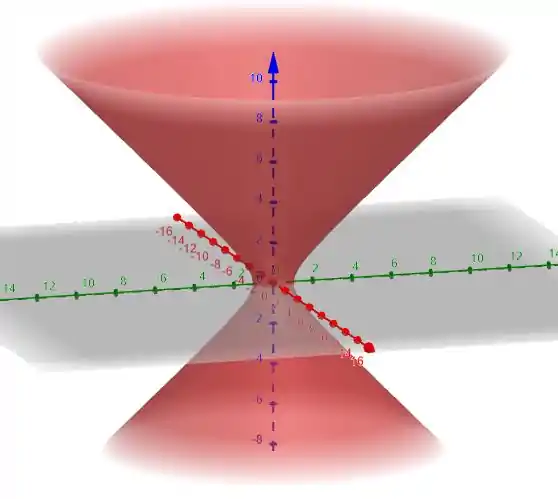
Resposta
Respondido acima!