Desenhe as superfícies nos Exercícios 13-44.
26.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Fazendo a equação do cone em uma forma padrão para desenhá-la
Dividindo todo mundo por 36
Simplificando os termos, nós temos que
Passando para a forma canônica
Note que quando estamos mexendo com o plano (colocando na equação), temos apenas a origem, portanto, a origem é o vértice do cone. Já no plano nós temos duas retas e no plano , nós também temos duas retas . Em qualquer plano perpendicular ao eixo (colocando na equação), temos os dois círculos.
Passo 2
Da discussão acima, a equação dada representa um cone elíptico reto de vértice , ao longo do eixo e com intersecção com o plano e nas duas linhas e as duas linhas respectivamente. Portanto, o gráfico é o mostrado abaixo.
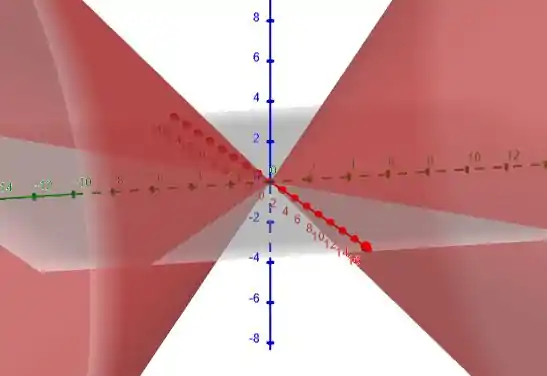
Resposta
Respondido acima!