Desenhe as superfícies nos Exercícios 13-44.
35.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Fazendo a equação paraboloide em uma forma padrão para desenhá-la
Passando para a forma padrão
Vamos observar que o vértice está localizado em (0,0,0). No plano xy (colocando na equação), temos a parábola . No plano (colocando na equação), temos a parábola .
Nos planos , temos os círculos que são perpendiculares ao eixo .
Passo 2
Da discussão acima, a equação dada representa um paraboloide circular reto, cujo vértice está em (0,0,0) e tendo as duas parábolas e abrindo na direção de ao longo do eixo .
Portanto, o gráfico é o mostrado abaixo.
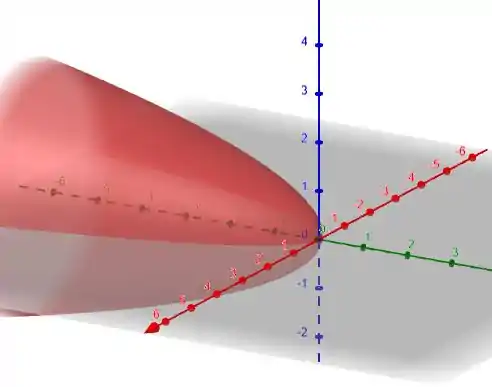
Resposta
Respondido acima!