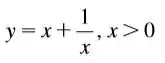Determine a função cujo gráfico passa pelo ponto e que goza da propriedade: a área do triângulo de vértices e é igual a , para todo no gráfico de , onde é a interseção da reta tangente em com o eixo .
Passo 1
Belezinha galera, vamos lá! Seja
![]()
A função procurada. A equação da reta tangente no ponto genérico:
![]()
É:
![]()
Passo 2
Para que a reta tangente encontre o eixo no ponto , deveremos ter, como, a área do triângulo de vértices e é , segue que a função procurada é solução da equação
Que é equivalente a , ou seja, a função procurada , deverá ser solução da equação linear .
Passo 3
Resolvendo e levando em conta a condição para obtém-se: