Passo 1
- Primeiro queremos encontrar a posição da partícula nos instantes e .
- Para esboçar a trajetória iremos inicialmente separar as componentes de em , e .
- Vamos fazer uma breve análise aqui:
Aqui é fácil, basta substituir os valores no seu vetor posição que foi dado.
- Para :
- Para :
Passo 2
Agora iremos definir um limite arbitrário (respeitando o domínio das componentes) para montar uma tabela auxiliar no esboço da trajetória.

Agora basta marcar os pontos que achamos e traçar nosso esboço!
Para
Para
Para
Para
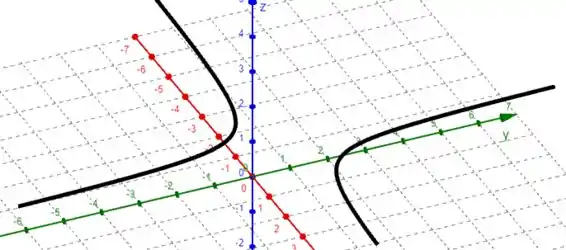
Passo 3

Perceba que quanto mais nos aproximamos de pela esquerda, menor o valor de e quanto mais nos aproximamos de pela direita, maior o valor de .
Isso significa que, quando e .
Isso também pode ser observado apenas por análise gráfica!
Resposta
- Resposta nos passos acima.
- Quando e .