Passo 1
- Escrever :
- Vamos determinar nosso vetor velocidade e aceleração de .
- No instante temos:
Observe que os valores das componentes e já foram dados. Basta reescrever:
Logo,
Passo 2
Para o cálculo da velocidade, vamos fazer a derivada primeira do nosso vetor:
Logo,
Para o cálculo da aceleração, vamos fazer a derivada segunda do nosso vetor:
Logo,
Passo 3
- Para a trajetória da partícula:
O esboço fica
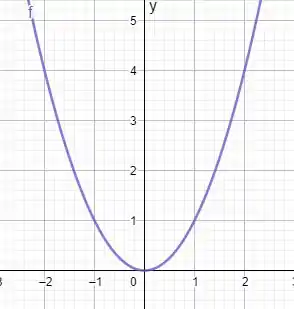
Em :
Logo,
- Para a velocidade:
O esboço fica
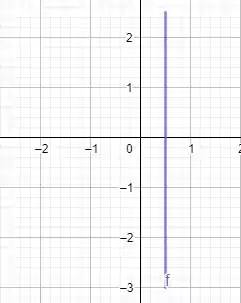
Em :
Logo,
- Para a aceleração:
O esboço fica
Em :
Logo,
Resposta
a)
b)
c)
Com os esboços nos passos acima.