Passo 1
Fala, galeeera!
Vamos esboçar o gráfico dessa curva para . Essa parte é fácil, né?
Vou montar uma tabelinha para ajudar a gente:

Agora é só traçar os pontos e esboçar nosso gráfico:
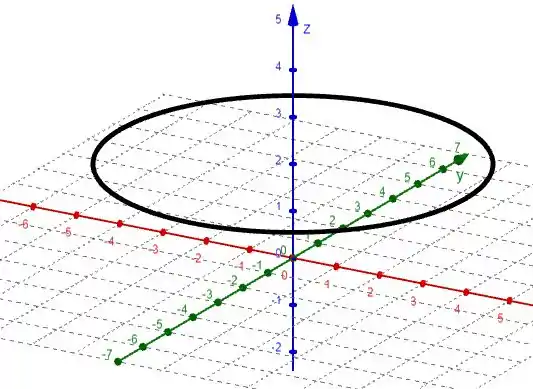
Passo 2
Nessa parte ele tá pedindo pra gente determinar a equação CARTESIANA da curva.
Bem, já nos foi dada a equação paramétrica da nossa curva.
Olhando para elas, já conseguimos notar que parece muuuito com as equações paramétricas de uma circunferência, certo?
E também já sabemos que a equação cartesiana de uma circunferência é dada por:
Onde, raio, e são as coordenadas do centro da circunferência.
E temos que, em coordenadas polares:
Relembrando tudo isso, podemos seguir com a nossa resolução!
Assim, conseguimos notar que e , ou seja, seu centro coincide com a origem.
Além disso, identificamos o nosso .
Logo,
Como já sabemos como é nossa equação cartesiana da circunferência, é só substituir os valores que encontramos!
Logo,
Masss, temos uma informação muito importante que temos que considerar!
Ou seja, estamos trabalhando no espaço (3 dimensões)!
Então a nossa curva é o cilindro interceptado pelo plano .
Essa é a nossa equação cartesiana.
Resposta
Esboço do gráfico descrito nos passos acima.
A equação cartesiana é: