Passo 1
Pessoal, primeiro queremos identificar qual curva é essa.
A primeira coisa a ser feita é completar quadrados para ver como a nossa equação fica. Assim, facilita muuuuuito na identificação da curva. Bora lá?!
Agrupando e e passando a constante para o lado direito da equação:
Completando quadrados:
- Lembrando que:
Antes de completar os quadrados, vamos multiplicar os dois lados da nossa equação por para facilitar a análise:
Usando esta relação, sabemos que:
Logo:
Essa equação se parece muuuito com a equação da circunferência, né? Olha só:
É isso mesmo!
Temos a equação da circunferência com raio e centro .
Passo 2
Agora vamos parametrizar a nossa circunferência.
A equação vetorial da circunferência é dada por:
Fazendo as substituições:
E nossa parametrização fica com essa carinha aqui:
Sem mistério!
Passo 3
Finalmente (!!!!!) vamos esboçar nosso gráfico. Para isso, devemos ter em mente que . A gente pode montar nossa tabelinha pra ajudar no esboço, dentro deste intervalo, beleza?
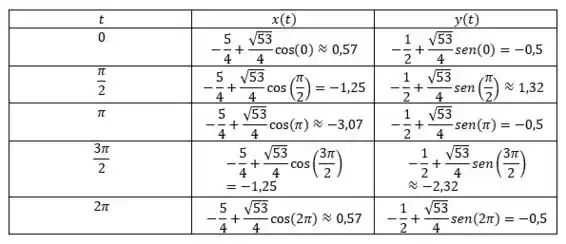
Agora basta traçar os pontos e esboçar nosso gráfico:
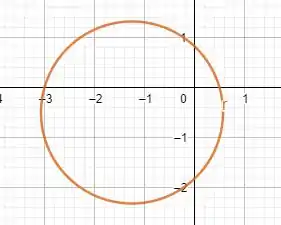
Resposta
A curva é uma circunferência.
Sua parametrização é dada por:
E seu esboço é mostrado nos passos acima.