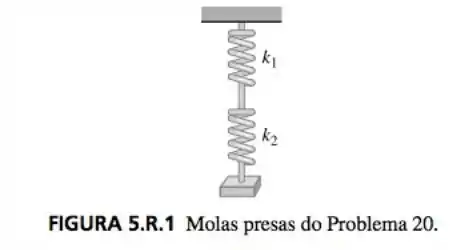
- Duas molas são presas em serie conforme mostra a figura 5.R.1. ignorando a massa de cada mola mostre que a constante k do sistema é dada por
- Uma massa pesando W libras estica uma mola em e uma outra diferente, em As duas molas são presas, e a massa é então presa à mola dupla como mostra na figura 5.R.1. Suponha que o movimento seja libre e que não haja nenhuma força de amortecimento, supondo que a massa será inicialmente solta em um ponto 1 pé abaixo da posição e equilíbrio a uma velocidade de para baixo.
- Mostre que a velocidade máxima da massa é
Passo 1
Faaaala, cara! Tranquileba?
No item b) achamos que a equação que o movimento desse sistema é:
(LINDO, NÃO?! NÃO!!! AHAHHAH)
Passo 2
Sabemos que a velocidade é a derivada da posição com respeito ao tempo. Assim:
Passo 3
E é máximo quando:
Portanto:
E está provado.
Resposta
Ei, a resposta está no passo a passo :)