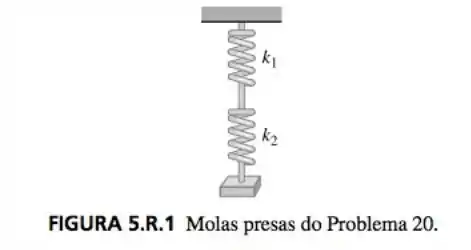
- Duas molas são presas em serie conforme mostra a figura 5.R.1. ignorando a massa de cada mola mostre que a constante k do sistema é dada por
- Uma massa pesando W libras estica uma mola em e uma outra diferente, em As duas molas são presas, e a massa é então presa à mola dupla como mostra na figura 5.R.1. Suponha que o movimento seja libre e que não haja nenhuma força de amortecimento, supondo que a massa será inicialmente solta em um ponto 1 pé abaixo da posição e equilíbrio a uma velocidade de para baixo.
- Mostre que a velocidade máxima da massa é
Passo 1
Faaaala, cara! Tranquileba?
Temos que:
E
E provamos no item a) que logo
E lembrando que W é peso, logo a sua massa é podemos fazer nossa EDO:
Passo 2
Vemos que E façamos desse valor igual a , ou seja,
Assim:
Fazendo
Logo
usemos a relação de Euler- De Moivre: . Assim:
Fazendo
Onde e são definidos pelas condições iniciais.
Passo 3
- É dito que a massa é solta da posição de 1 pé abaixo da posição de equilíbrio, logo
- É também dito que ela parte com uma velocidade de para baixo, logo
De modo que:
Assim:
Lembrando que
Que pode ser escrito de forma igual a:
Resposta
Ou