Encontre a área dos triângulos cujos vértice são dados nos exercícios 41-47.
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora!
Temos que um dos encontros de vértice do paralelogramo, é a subtração das coordenadas do ponto escrito depois menos o ponto escrito antes. Por exemplo no caso, de:
É a subtração das coordenadas de B menos as coordenadas de A. Dessa forma:
Já a outro encontro é formado por
Para obtermos então a área, precisamos fazer . Isso gera a seguinte matriz:
E agora, precisamos achar o determinante dela.
Passo 2
Show, para achar o determinante de uma matriz 3x3, temos o seguinte modelo:
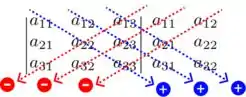
Então, vamos seguir as setas em azul realizando o produto dos elementos na mesma seta, e SOMANDO com a o produto da próxima seta e por aí vai. Para as setas em vermelho, vamos realizar o produto dos elementos na mesma seta e SUBTRAIR. Ou seja, o determinante da matriz vai ser calculado por:
Traduzindo pra questão, temos a matriz:
O determinante dela pode ser calculado como:
Sendo o módulo:
Calculando a área, para um triangulo, temos que: