Encontre equações para os planos nos Exercícios 21-26.
O plano que passa por .
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora!
Chamando cada ponto desse de, respectivamente, , teremos as seguintes direções para o nosso plano:
Ou seja, temos que:
Para encontrar a equação desse plano, podemos fazer a matriz gerada pelos dois vetores. Temos então:
Show, para achar o determinante de uma matriz 3x3, temos o seguinte modelo:
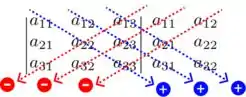
Então, vamos seguir as setas em azul realizando o produto dos elementos na mesma seta, e SOMANDO com a o produto da próxima seta e por aí vai. Para as setas em vermelho, vamos realizar o produto dos elementos na mesma seta e SUBTRAIR. Ou seja, o determinante da matriz vai ser calculado por:
Passo 2
Dessa forma, o determinante para essa matriz vai ser:
Seguinte, para montar a equação do plano, vamos utilizar os coeficientes das coordenadas do plano ao qual ele é normal. Esses vão ser também nossos coeficientes multiplicadores. Temos então, respectivamente .
Já as coordenadas do ponto pelo qual o plano passa, vamos subtrair de cada direção. Feito isso, vamos calcular assim:
Agora ficou fácil, só simplificar! Então temos:
Espero que tenham curtido! Até a próxima questão 😊