Encontre uma fórmula concisa para a área de um triângulo no plano xy com vértices (a1, a2), (b1, b2) e (c1, c2).
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Temos que, se:
Dessa forma, temos que, a área do triangulo é dada por:
Por sua vez,
Dessa forma, temos que:
Dado pelo determinante.
Passo 2
Show, para achar o determinante de uma matriz 3x3, temos o seguinte modelo:
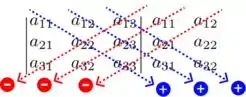
Então, vamos seguir as setas em azul realizando o produto dos elementos na mesma seta, e SOMANDO com a o produto da próxima seta e por aí vai. Para as setas em vermelho, vamos realizar o produto dos elementos na mesma seta e SUBTRAIR. Ou seja, o determinante da matriz vai ser calculado por: