Encontre o ponto de interseção das retas x = t, y = – t + 2, z = t + 1 e x = 2s + 2, y = s + 3, z = 5s + 6 e, em seguida, Defina o plano determinado por essas retas.
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Aqui, temos o sistema formato pelas retas. Dessa forma, fazendo um sistema para encontrar e :
Para isso, temos então que:
Logo,
Passo 2
A partir disso, temos que,
Aplicando os valores que achamos de e , a equação é satisfeita. Portanto, as retas se cruzam quando t =0 e s= -1 Ê o ponto de interseção é
Um vetor normal ao plano determinado por essas retas é
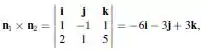
Onde e são as dimensões das linhas, no caso um plano de equação:
Espero que tenham curtido! Até a próxima questão 😊