Encontre o termo geral da série e use o teste da razão para mostrar que a série converge.
![]()
Passo 1
Um bom método de resolver essa questão é analisar a série, por exemplo, os numeradores são termos crescente, porém variam de duas em duas unidades, uma observação é que os valores são ímpares, ou seja, é como se tivéssemos um valor múltiplo de um número desconhecido e depois subtraíssemos uma unidade, como: .
Passo 2
Já nos denominadores temos termos fatoriais e, assim como os numeradores, variam de duas em duas unidades, além de também serem valores ímpares, ou seja, é como se tivéssemos um valor múltiplo de um número desconhecido e depois subtraíssemos uma unidade, como:
Logo, a equação geral da série é:
Passo 3
O comando da questão pede que apliquemos o teste da razão na equação geral, para isso colocaremos a equação geral da série no modelo:
Usando a série dada, temos os termos:
1)
2)
Logo:
Portanto,
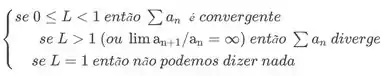
Logo, sendo L≤0, a série converge.
Resposta
Converge para