A equação logística para a população (em milhares) de uma certa espécie é dada por
a) Esboce o campo de direção usando ou um software de computador ou o método das isóclinas.
b) Se a população inicial é 3.000 [ou seja, p(0) = 3], o que você pode dizer sobre a população limitante limt → + ∞ p(t)?
c) Se p(0) = 0,8, o que é limt → + ∞ p(t)?
d) Uma população de 2.000 pode diminuir para 800?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- O campo de direção é o seguinte.
- Se a população inicial for de 3.000, então ela diminui e se aproxima de 1.500 do lado superior.
- Se a população inicial for 800, então ela aumenta e se aproxima de 1500 do lado inferior.
- Uma população de 2.000 diminuirá e tenderá a se estabelecer em 1.500. Portanto, nunca poderá diminuir para 800.
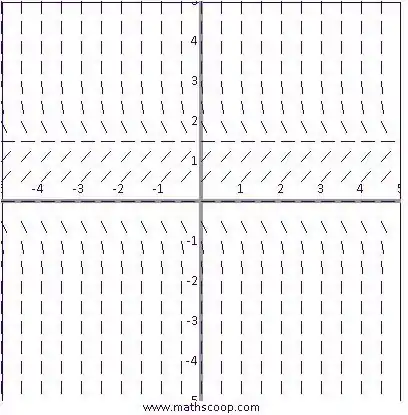
Observe no gráfico que quando a população é maior que 1500, então é negativo e, portanto, a população diminui até se tornar igual a 1500. Da mesma forma, se a população for diferente de zero e menor que 1500, então aumenta até se tornar igual a 1500. Ou seja, limt→∞p(t)=1500.
Passo 2
Resposta
A chave para a solução é que e