Esboçar o hodógrafo da seguinte função vetorial:
Passo 1
Fala, galeeera!
Primeiro devemos observar que estamos trabalhando em 3 dimensões, ou seja, no espaço, pois o aparece.
Para fazermos este esboço temos que ter em mente que o hodógrafo de coincide com a sua trajetória. Agora ficou fácil, né?!
Basta observarmos que os pontos do hodógrafo de tem coordenadas:
Passo 2
Para facilitar nossa vida, podemos fazer uma tabelinha em função de , e para determinar os pontos e traçar nosso esboço.
Repare que não temos uma região limitada para esboçar o gráfico, então iremos arbitrariamente definir que .

Passo 3
Agora basta marcar os pontos que achamos e traçar nosso esboço!
Para
Para
Para
Para
Para
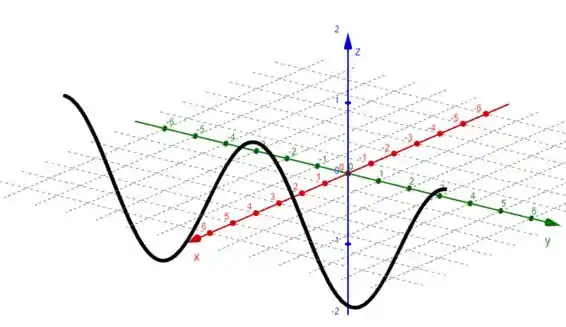
Resposta
Resolução nos passos acima.