Esboçar o hodógrafo da seguinte função vetorial:
Passo 1
Fala, galeeera! Essa é muito parecida com a questão anterior, porém o nosso não é nulo desta vez, logo, estamos trabalhando em 3 dimensões (no espaço)!
Para fazermos este esboço temos que ter em mente que o hodógrafo de coincide com a sua trajetória. Agora ficou fácil, né?!
Basta observarmos que os pontos do hodógrafo de tem coordenadas:
Passo 2
Para facilitar nossa vida, podemos fazer uma tabelinha em função de , e para determinar os pontos e traçar nosso esboço.
Reparem que no enunciado temos uma informação valiosíssima: , ou seja, nossa tabela vai ficar entre esses pontos apenas!
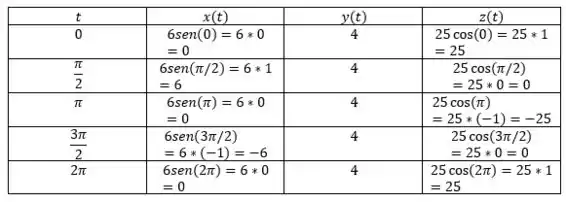
Passo 3
Agora basta marcar os pontos que achamos e traçar nosso esboço!
Para
Para
Para
Para
Para
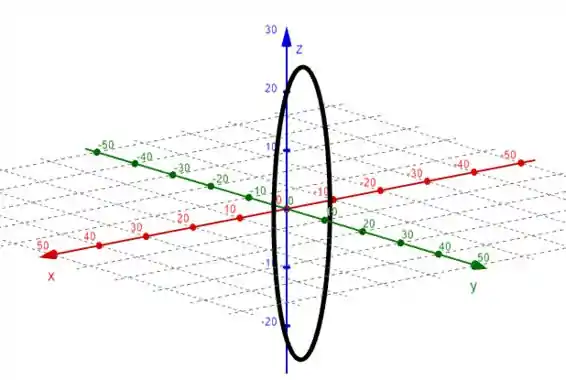
Resposta
Resolução nos passos acima.