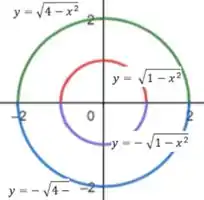
(a) Esboce algumas curvas integrais típicas da equação diferencial y’ = -x/y
(b) Determine uma equação da curva integral que passe pelo ponto (3,4)
Passo 1
Para esboçarmos o gráfico, primeiro temos que ter uma equação que será obtida pelo método da separação de variáveis.
Começamos colocando a equação no modelo: , sendo que cada termo deve ser dependente de apenas uma variável. Assim, na equação dada, substitui-se e arrumam-se os termos:
O próximo passo é integrar os dois lados da igualdade
Elevamos os dois lados da equação à função logarítmica para isolarmos o y:
Passo 2
A partir da equação (1), podemos aplicar valores positivos e negativos para “C” e obter diferentes curvas. A tabela a seguir mostra alguns valores típicos de “C”:
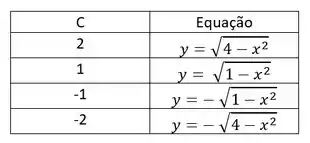
Depois disso, basta aplicar essas equações em um recurso computacional e obteremos as seguintes curvas
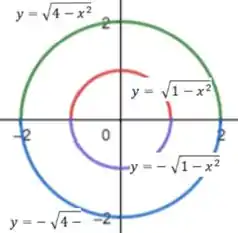
Passo 3
Para determinarmos a equação que intercepta o ponto (3,4), basta substituir a coordenada na equação (1) para descobrir o valor de “C”.
E por fim, substituímos o “C” na equação (1):
Resposta
a)