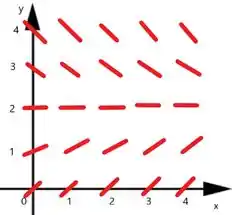
Esboce o campo de direções para y + y = 2 nos 25 pontos de malha (x, y), dados por x = 0, 1,..., 4 e y = 0, 1,..., 4.
Passo 1
Para esboçar o campo de direções podemos atribuir valores de x e y. O valor de y’ representa a inclinação do campo de direções.
Passo 2
Analisando a equação dada, percebemos que a derivada depende apenas de “y”, logo, é necessário achar uma solução de equilíbrio que ocorre quando y’=0, nesse ponto o ângulo de inclinação é zerado, portanto:
A partir disso, teremos que fazer duas análises, considerando y = {0,1,2,3,4}
Se y > y*
Se y
Passo 3
E assim por diante, as coordenadas vão sendo trocadas até atingir os 25 pontos de malha para determinar o valor do ângulo de inclinação.
Por fim, podemos esboçar o seguinte campo de inclinação correspondente
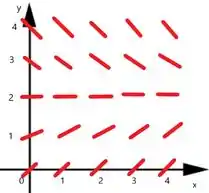
Resposta