Esboce a curva integral de 2yy’ = 1 que passa pelo ponto (0, 1) e a curva integral que passa pelo ponto (0, −1).
Passo 1
Para esboçarmos o gráfico, primeiro temos que ter uma equação que será obtida pelo método da separação de variáveis.
Começamos colocando a equação no modelo: , sendo que cada termo deve ser dependente de apenas uma variável. Assim, na equação dada, substitui-se e arrumam-se os termos:
O próximo passo é integrar os dois lados da igualdade
Passo 2
Em seguida aplica-se às coordenadas que o comando sugere a curva trace, aplicamos duas vezes na equação (1) pois são duas coordenadas, o objetivo é determinar o valor da variável “C”, temos:
- Se (0, 1)
- Se (0, -1)
Passo 3
Os valores de ”C” são substituídos na equação 1 e, apesar de serem iguais, geram equações de valores opostos, isso ocorre porque os valores empregados ao “y” foram negativo e positivo, assim, temos:
Plotamos as equações (2) e (3) que satisfazem as condições da questão e obtemos a seguinte curva
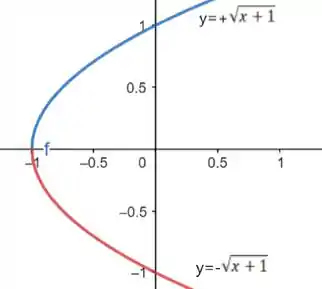
Resposta