Esboce a curva de nível de que passa por e desenhe o vetor gradiente em .
Passo 1
Primeiramente, vamos encontrar
De posse desse valor, vamos achar a função da curva de nível igualando o resultado de com a função .
Vamos observar que a função da curva de nível é uma parábola. Isso vai ajudar lá na frente.
Passo 2
Para encontrar e na coordenada , faremos a derivação e a substituição do valores do ponto, assim temos:
Passo 3
Agora, de posse dos valores de e vamos aplicar a formula de
Passo 4
Por fim, vamos para o desenho da curva de nível e o vetor gradiente.
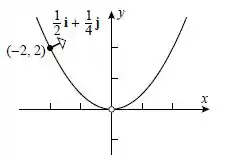
De boa, né?