Esboce o gráfico da solução da equação
que satisfaz a condição inicial dada.
a)
Passo 1
Queremos resolver a EDO linear de primeira ordem
que é do tipo
Para resolver esse tipo de equação, achamos o fator integrante:
Como :
Multiplicando a equação por esse fator:
Passo 2
Note que o lado direito é fatorado como
Assim,
Integrando dos dois lados:
Passo 3
Para calcular essa integral, usamos integração por partes:
Chamando e :
Assim,
Com isso,
Logo,
Ou ainda,
Passo 4
Usando a condição inicial
temos que
Logo,
Portanto,
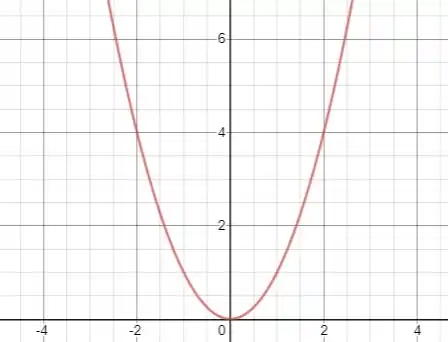
O gráfico é a parábola: