Dê uma estimativa para .
Passo 1
Fala, pessoal!!!
Já sabemos que a estimativa da derivada se dá por:
Substituindo
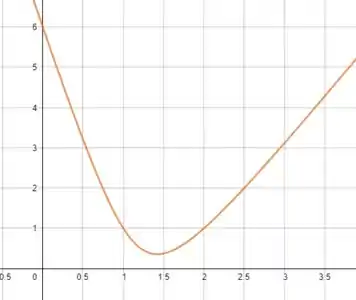
Vamos fazer um teste pra valores onde conseguimos identificar os menores valores de só de olhar para o gráfico, beleza?
Vamos usar os pontos: e .
Onde,
Montando uma tabelinha para facilitar nossa vida:

Fazendo a média desses valores, que no caso é a média das derivadas antes e depois do ponto onde , podemos ver a tendência de quando se aproxima de :