No exercício 11, determine o domínio de cada função

Passo 1
Eaew, como vai, tudo certinho?
Precisamos analisar qual o domínio destas funções, isso se resume a analisar para quais valores da variável (neste caso ) temos que é bem definida. Usualmente é mais fácil procurar por pontos onde as coisas não funcionam muito bem, beleza? Então vamos que vamos!
Passo 2
Temos que a função dada é tal que:
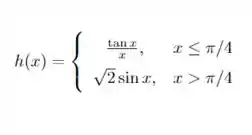
Note que no primeiro intervalo a função é bem comportada para todo valor de contanto que e que , pois lembre que:
Por si só, isto nos daria um domínio da forma:
No entanto, se , temos que pertence ao intervalo posterior que não apresenta nenhum problema de definição, portanto, todos os valores inteiros positivos para são válidos, mas ainda temos problemas para todos os inteiros negativos, ou seja:
Resposta
A resposta está ao longo do passo 2.