Nos Exercícios 49-52, encontre o intervalo no qual a função é crescente.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Uma função está aumentando se:
Uma função está diminuindo se:
Passo 2
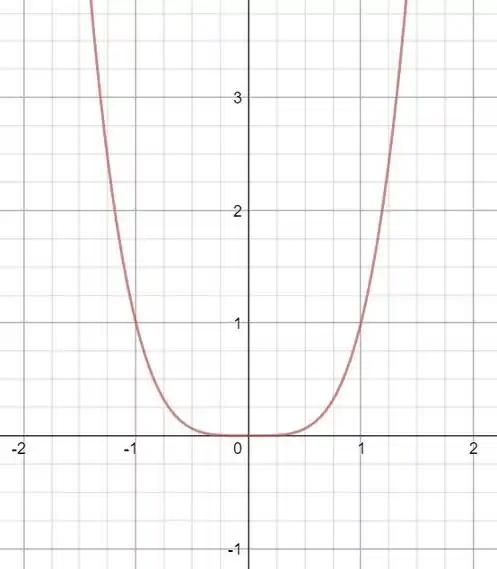
A função é uma função de poder com um poder uniforme.
O zero desta função está em x=0
Discutiremos a função em dois intervalos diferentes (−∞,0) e (0,∞) e escolheremos , de tal forma que e e pertencem a .
A função está diminuindo no intervalo (-, 0)
Escolher de tal forma que e pertencer
A função está aumentando no intervalo (0,∞)
Resposta
A função está aumentando no intervalo (0,∞)