Nos Exercícios 9-32, determine os números críticos e os intervalos abertos nos quais a função é crescente ou decrescente. Então, use uma ferramenta gráfica para traçar o gráfico da função.
Passo 1
Determinaremos os pontos críticos a partir da derivada igual a zero e descobriremos em quais pontos ela se anula. Então,
Nos fornecendo um ponto crítico e necessitando de dois intervalos de teste, onde temos: e .
Passo 2
Agora que sabemos os intervalos de teste, vamos testar se é positivo ou negativo nesses intervalos. Como , pois números elevados ao quadrado são sempre positivos. Ou seja, esse termo quadrático garantirá o sinal positivo da derivada função para qualquer valor de .
Passo 3
O gráfico da função pode ser visto abaixo e corresponde ao que encontramos nos nossos cálculos.
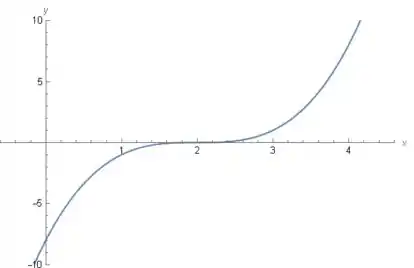
Resposta
é crescente nos intervalos e , com número crítico em .