Nos Exercícios 9-32, determine os números críticos e os intervalos abertos nos quais a função é crescente ou decrescente. Então, use uma ferramenta gráfica para traçar o gráfico da função.
Passo 1
Para obter os números críticos e intervalos abertos nos quais a função é crescente ou decrescente seguimos sempre o mesmo roteiro: calculamos a derivada da função, vemos para quais valores essa derivada é nula, descobrimos os intervalos de teste, vemos o crescimento da função nesses intervalos através do sinal da derivada.
Então, sem mais delongas, vamos calcular a derivada e obter os pontos críticos:
será sempre constante e igual a . Então, essa função não tem pontos críticos. Mas isso não significa que não podemos testar seu crescimento, mas sim que o único intervalo de teste será .
Passo 2
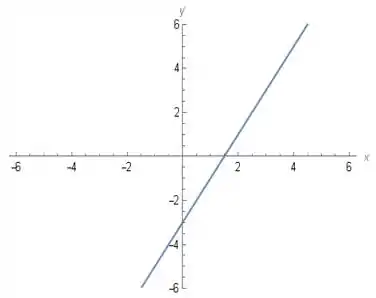
Nesse caso, sempre teremos , ou seja, a função é sempre crescente, não importando qual seja o intervalo. O gráfico da função, obtido no Wolfram Alpha, é dado abaixo:
Resposta
é sempre crescente em .