Nos Exercícios 9-32, determine os números críticos e os intervalos abertos nos quais a função é crescente ou decrescente. Então, use uma ferramenta gráfica para traçar o gráfico da função.
29.
Passo 1
E vamos que vamos para mais uma resolução. A função é polinomial, ou seja, ela é representada por termos do tipo . Então para calcular a derivada dessa função, temos que lembrar da fórmula . Agora ficou mais fácil, né? Olha só como vai ficar a derivada:
Passo 2
Tudo certinho até agora? Então vamos continuar calculando os números críticos, que são os pontos onde a derivada se anula. Assim, temos uma equação de 3º grau . Vamos tentar manipular essa equação para obter suas raízes
Nesse caso, devemos ter ou . No primeiro caso, temos e no segundo temos . Então esses são os números críticos da função. Além disso, vamos ter três intervalos de teste: , e . Para saber se a função é crescente ou decrescente, temos que saber se a derivada é positiva ou negativa num intervalo. Como um número elevado ao quadrado sempre tem resultado positivo ou nulo, isto é , então só temos que testar o sinal de :
A derivada é negativa no intervalo. Logo, a função é decrescente no intervalo.
Nesse intervalo, a derivada também é negativa, o que significa que a função é decrescente.
Nesse caso, a derivada é positiva, então a função é crescente
Passo 3
No passo anterior descobrimos que a função é decrescente em e (ou seja, decrescente no intervalo ) e crescente em . O gráfico da função, abaixo, mostra justamente isso e podemos notar que é o ponto em que a função deixa de ser decrescente e passa a ser crescente. Apesar de ser um número crítico, a função não muda seu comportamento nesse ponto.
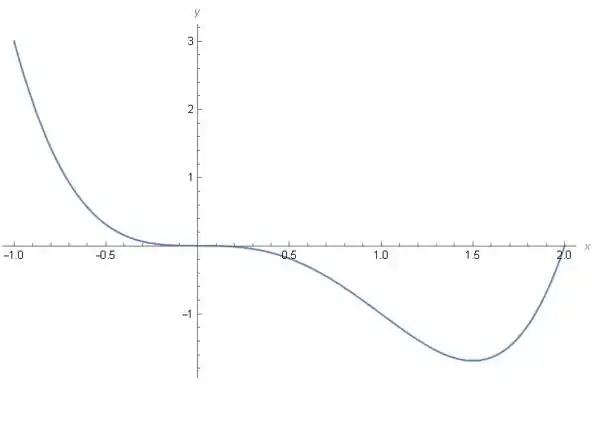
Resposta
Pontos críticos e , decrescente em e crescente em .