Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
10.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Temos que reformar nossa equação para torná-la de uma forma semelhante às formas padrão, como segue
Invertendo os sinais
Simplificando um pouco mais os termos, nós temos que
Deixando na forma canônica
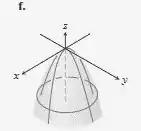
Da última equação, nossa equação representa um parabolóide elíptico ao longo do eixo e este parabolóide abre para baixo porque se colocarmos em (1), obtemos parábolas ao longo dos eixos paralelos ao eixo z abrindo para baixo e se colocarmos em (1), obtemos parábolas ao longo de eixos paralelos ao eixo abrindo para baixo.
Como temos apenas um parabolóide elíptico abrindo para baixo ao longo do eixo z entre os gráficos fornecidos temos (f), por isso nós o escolhemos.
Resposta
Respondido acima!