Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
6.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Este exercício visa que, com base na equação dada:
Com isso, identificar a superfície por tipo. Então, vamos reescrever a equação dada em uma forma que possamos identificar facilmente. Se está em um lado da equação e a diferença de e está no outro lado, então esta é a equação de um parabolóide hiperbólico.
A equação quadrática que contém termos quadráticos nas duas variáveis com coeficientes do mesmo sinal, apenas termos lineares em uma das variáveis, e nenhum termo constante, é um parabolóide elíptico. Em nossa equação, e têm os coeficientes do mesmo sinal, apenas o termo linear é e não há termo constante. Portanto, assumimos que nossa equação descreve o parabolóide elíptico. A forma é descrita como
Passo 2
A variável que não é quadrada determina o eixo sobre o qual o parabolóide se abre. Além disso, o sinal de determina a direção que o parabolóide abre. No caso que:
Abre no sentido positivo e no caso:
Abre no sentido negativo. A equação dada pode ser expressa da seguinte forma:
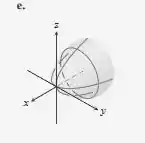
Como notamos, esta equação tem a forma dada acima com e . Como e representam a variável que não é quadrada, podemos concluir que o eixo é o eixo sobre o qual o parabolóide abre e que abre na direção negativa. Assim, a equação dada descreve o parabolóide elíptico que é mostrado na parte (e).
Resposta
Respondido acima!