Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
3.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Temos que reformar nossa equação para torná-la de uma forma semelhante às formas padrão, como segue
Dividindo todo mundo por , obtemos que
Simplificando um pouco mais
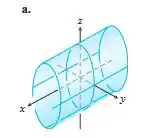
Da última equação, nossa equação representa um cilindro elíptico ao longo do eixo x com a elipse , com no plano . Como temos apenas um cilindro elíptico ao longo do eixo em (a) entre os gráficos fornecidos, escolhemos o cilindro elíptico (a).
Resposta
Cilindro elíptico (a)