Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
8.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Este exercício visa no que é baseado na equação do enunciado
E com isso, identificar a superfície por tipo. Então, vamos reescrever a equação dada em uma forma que possamos identificar facilmente. O menos na frente de nos diz que o eixo é o eixo de simetria. Os traços da superfície que é dado pela equação acima são elipses no plano .
Enquanto são hipérboles no plano e no plano .
E
Assim, com base nas conclusões acima, notamos que a equação dada se assemelha à equação de um hiperbolóide de uma folha. Vamos primeiro relembrar a equação geral do hiperboloide de uma folha.
Passo 2
Como notamos, a equação dada pode ser expressa na forma dada acima:
Com e . Notamos que a interceptação de nossa hiperbólica de uma folha com eixo e eixo são pontos e , enquanto não há interseção com o eixo porque se definirmos e em nossa equação, obtemos:
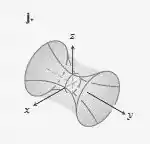
Esta situação não admite solução real para o termo de . Considerando as superfícies dadas, notamos que são dados dois hiperbolóides de uma folha. Notamos que não há interseção do hiperbolóide de uma folha na parte (i) com o eixo x, enquanto não há interseção do hiperbolóide de uma folha na parte (j) com o eixo y. Assim, podemos concluir que a equação dada descreve o hiperbolóide de uma folha mostrada na parte (j).
Resposta
Respondido acima!