Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
9.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Este exercício visa que, com base na equação dada:
Com isso, vamos identificar a superfície por tipo. Então, vamos reescrever a equação dada em uma forma que possamos identificar facilmente. Se está em um lado da igualdade e a soma de e está no outro lado, então esta equação é a equação do parabolóide elíptico. A equação quadrática que contém termos quadráticos nas duas variáveis com coeficientes de sinais diferentes, apenas termos lineares em uma das variáveis, e nenhum termo constante, é um parabolóide hiperbólico.
Em nossa equação, e têm coeficientes de sinais diferentes, apenas o termo linear é e não há termo constante. Portanto, assumimos que nossa equação descreve o parabolóide hiperbólico. Que é definida pela seguinte equação
Este parabolóide hiperbólico é simétrico em relação ao plano e ao plano . As seções do parabolóide hiperbólico com planos paralelos ao plano ou ao plano são parábolas, enquanto as seções com planos paralelos ao plano são hipérboles.
Passo 2
A equação dada pode ser expressa da seguinte forma:
Como notamos, a equação dada pode ser expressa na forma dada acima com e . Considerando as superfícies dadas, notamos dois parabolóides hiperbólicos.
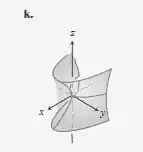
As seções do parabolóide hiperbólico na parte (l) com planos paralelos ao plano ou ao plano são parábolas enquanto as seções com planos paralelos ao plano são hipérboles. As seções do parabolóide hiperbólico na parte (k) com planos paralelos ao plano ou ao plano são parábolas enquanto as seções com planos paralelos ao plano são hipérboles.
Assim, podemos concluir que a equação dada descreve o parabolóide hiperbólico fornecido na parte (k).
Resposta
Respondido acima!