Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l.
1.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Temos que reformar nossa equação para torná-la de uma forma semelhante às formas padrão, como segue
Dividindo os dois lados por 10
Elevando todo mundo ao quadrado
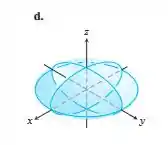
Da última equação, nossa equação representa um elipsóide de revolução porque possui dois semi-eixos iguais a e b. Como temos apenas um elipsóide de revolução (d) nos gráficos fornecidos, escolheremos o elipsóide em (d). Observe que se colocarmos z=0 em (1), obtemos um círculo no plano xy como em (d).
Passo 2
O elipsóide é descrito da seguinte forma
Resposta
Elipsóide na letra d)